skiplist - 跳表 | 一七令

前言

跳表(skiplist、跳跃表) 是一个很优秀的数据结构，比如用于 Redis、levelDB等出名的开源项目上。跳表在原有的有序链表上面增加了多级索引，通过索引来实现快速查找。

它的结构特点在名称能很好的体现出来，就像兔子一样，蹦蹦跳跳。可以结合下面的图有个初步的印象。

在这里插入图片描述

是不是看起来很形象了，接下来看看 Redis 是怎么实现跳表。

源码解读

本文讲解的版本为 Redis 6.0 ，可以在 server.h 头文件中找到对 skiplist 结构的定义。在 Redis 中，目前使用到跳表的只有有序集合(zset)。

定义结构体处有段注释，也指明了跳表在 Redis 中的使用范围了。

ZSETs use a specialized version of Skiplists

// 有序集合的结构体
typedef struct zset &#123;
    dict *dict;  // 哈希表是一种实现方式。
    zskiplist *zsl; // 本文主题 跳表 实现方式。
&#125; zset;

// 跳表结构体
typedef struct zskiplist &#123;
    struct zskiplistNode *header, *tail;  // zskiplistNode 跳表节点, *header, *tail 头尾指针 
    unsigned long length;  // 节点的数量
    int level; // 最大层数
&#125; zskiplist;

// 跳表节点结构体
typedef struct zskiplistNode &#123;
    sds ele;  // 成员对象
    double score;  // 分值   作为索引
    struct zskiplistNode *backward;   // 后退指针
    
    // 节点层结构 数组
    struct zskiplistLevel &#123;
        struct zskiplistNode *forward;  // 前进指针
        unsigned long span; // 该层向前跨越的节点数量
    &#125; level[];
&#125; zskiplistNode;

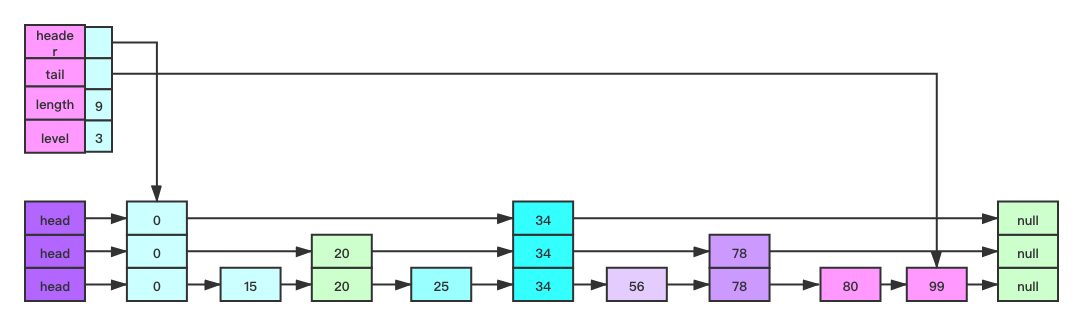
看完上面的注视相比大家脑海中也构建出一张图了，它应该是长的和下图差不。
在这里插入图片描述
比如现在需要查找元素 56。

若是普通的链表就需要遍历整个链表，直到找到为止。如上图就需要查找 6 次。

但在跳表中，首先判断节点 56 是大于 34，则去下一层。节点 56 < 节点 78，然后遍历节点 34～节点 78中间。这时候只有一个节点 56。所以需要查找 3 次就可以找到了。

操作接口

操作结构的实现在 t_zset.c 文件中（不像 ziplist、quicklist 等是同名的一组文件）。

创建跳表


zskiplist *zslCreate(void) &#123;
    int j;
    zskiplist *zsl; 

    zsl = zmalloc(sizeof(*zsl)); //  申请内存
    zsl->level = 1; // 默认层级
    zsl->length = 0;  // 默认长度
    
    // 头指针创建， ZSKIPLIST_MAXLEVEL 最大层级为 32，可容纳  2^64   个节点。
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    
    // 跳表结构的头节点需有足够的指针域，以满足可能构造最大级数的需要，而尾节点不需要指针域。
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) &#123;
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    &#125;
    
    //  上面遍历 32 次，生成下面这段结构。
    //   struct zskiplistLevel &#123;
    //       struct zskiplistNode *forward;  // 前进指针
    //       unsigned long span; // 该层向前跨越的节点数量
    //    &#125; level[];
  
   zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
    
&#125;

节点插入


zskiplistNode *zslInsert(zskiplist *zsl, double score, sds ele) &#123;
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    unsigned int rank[ZSKIPLIST_MAXLEVEL];
    int i, level;

    serverAssert(!isnan(score));
    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) &#123;
        
        // 遍历找到插入的位置
        rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                    sdscmp(x->level[i].forward->ele,ele) < 0)))
        &#123;
            rank[i] += x->level[i].span;
            x = x->level[i].forward;
        &#125;
        update[i] = x;
    &#125;
    
    // 调用 zslInsert 的地方需要在 hash 中判断当前插入的元素是否已经存在集合中。
    // 元素不能重复，但是元素的分数是可以重复的。
     
    // 生成随机值 代表需要插入的层级。 下面会讲解具体实现。
    level = zslRandomLevel();
    
    if (level > zsl->level) &#123;
        for (i = zsl->level; i < level; i++) &#123;
            rank[i] = 0;
            update[i] = zsl->header;
            update[i]->level[i].span = zsl->length;
        &#125;
        zsl->level = level;
    &#125;
    
    // 创建节点
    x = zslCreateNode(level,score,ele);
    for (i = 0; i < level; i++) &#123;
        x->level[i].forward = update[i]->level[i].forward;
        update[i]->level[i].forward = x;

         // 插入新节点后需要更新前后节点对应的span值。 span 是到下一个节点的跨度 
        x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);
        update[i]->level[i].span = (rank[0] - rank[i]) + 1;
    &#125;

    // 更新 其他level增加 span 值
    for (i = level; i < zsl->level; i++) &#123;
        update[i]->level[i].span++;
    &#125;
    
    // 更新 后退指针。
    x->backward = (update[0] == zsl->header) ? NULL : update[0];
    if (x->level[0].forward)
        x->level[0].forward->backward = x;
    else
        zsl->tail = x;
    zsl->length++;
    return x;
&#125;

// 这里需要单独说下这个随机值生成的规则。

int zslRandomLevel(void) &#123;
    int level = 1;
    // ZSKIPLIST_P = 0.25 ，虽然跳表的时间复杂度和二分查找一样，但是这里并不是 50% 的概率来控制一个节点是否放到下一层，而是 25%。 所以同一层节点下一层间的元素个数并不是一样的哦。
    // 还有的说法是这个值为 0.27更合适。 就是自然常数 e (2.7)。

    // random() 生成的随机数和 0xFFFF(16个1) 做 与运算。
    // 其实就是获取random()（32位）的前16位（或者说低位）。
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
&#125;

节点删除


int zslDelete(zskiplist *zsl, double score, sds ele, zskiplistNode **node) &#123;
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) &#123;
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                     sdscmp(x->level[i].forward->ele,ele) < 0)))
        &#123;
            x = x->level[i].forward;
        &#125;
        update[i] = x;
    &#125;
   
   // 找到分数和值都一样的元素。
    x = x->level[0].forward;
    if (x && score == x->score && sdscmp(x->ele,ele) == 0) &#123;
        zslDeleteNode(zsl, x, update);
        if (!node)
            zslFreeNode(x);
        else
            *node = x;
        return 1;
    &#125;
    return 0; // 没找到
&#125;

// 删除的具体逻辑
void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) &#123;
    int i;
    
    // 更新 每一层forward、span。
    for (i = 0; i < zsl->level; i++) &#123;
        if (update[i]->level[i].forward == x) &#123;
            update[i]->level[i].span += x->level[i].span - 1;
            update[i]->level[i].forward = x->level[i].forward;
        &#125; else &#123;
            update[i]->level[i].span -= 1;
        &#125;
    &#125;
    if (x->level[0].forward) &#123;
        x->level[0].forward->backward = x->backward;
    &#125; else &#123;
        zsl->tail = x->backward;
    &#125;
    // 若删除的层级没有元素 层级减 1。
    while(zsl->level > 1 && zsl->header->level[zsl->level-1].forward == NULL)
        zsl->level--;
        
    // 元素长度减 1。
    zsl->length--;
&#125;